Day 4 - AI Basic

벡터

벡터는 공간에서 한 점을 나타냄

벡터의 노름

벡터의 노름은 원점에서부터 거리를 의미함

L1 노름은 절댓값의 합으로 표현한다.

L1 노름

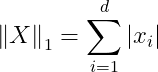
L2 노름은 유클리드 거리를 계산함.

L2 노름

 

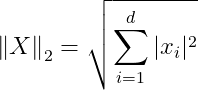
# 직접 구현
def l2_norm(x):
	x_square = x * x
    x_sum = np.sum(x_square)
    x_norm = np.sqrt(x_num)
    return x_norm
    
# np.linalg.norm 사용 (줄여서 LA.norm이라고도 하는 듯.)
np.linalg.norm(x, 2) # 뒤에 들어가는 인자는 l2노름임을 의미한다.

행렬

행렬은 벡터를 원소로 가지는 2차원 배열.

• 벡터를 공간에서 한 점이라고 한다면, 행렬은 여러 점들을 나타낸다고 할 수 있다.
• 벡터를 다른 차원의 공간으로 보내는 연산자로 이해 할 수 있다.

벡터를 행으로 쌓는 배열 = 행렬

유사역행렬 = 무어-펜로즈 역행렬

행과 열의 숫자가 같고 행렬식이 0이 아닌 경우에만 역행렬을 구할 수 있다.

역행렬을 구할 수 없을땐 유사 역행렬을 구하면 된다.

아래와 같이 구할 수 있다. 

n>=m 라는 의미는 위로 길쭉한 경우, n<=m라는 의미는 옆으로 길쭉한 경우를 말함.

# numpy에서 구할 수 있다.
numpy.linalg.pinv(X)

이를 통해 어떤 연립 방정식도 풀 수 있다.

 

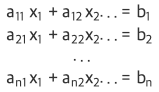
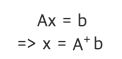
경사하강법

함수의 미분을 구해, 미분값이 0에 도달하는 지점을 찾는 방법이다.

아래와 같은 코드로 간단히 표현 할 수 있다.

grad = gradient(x) # 기울기
while abs(grad) > eps: # eps는 용인할 수 있는 최고 기울기
    x = x - lr * grad # lr은 학습률 (너무 작으면 학습이 오래 걸리고, 너무 크면 학습이 잘 안된다.)
    grad = gradient(x)

변수가 여러개라면?

변수가 벡터일때는 편미분을 구해서 풀이한다.

각각 벡터 원소의 편미분을 구한 벡터를 그레디언트 벡터라고 한다.

그레디언트-벡터

선형회귀 계수 구하기

선형회귀의 목적은 오차를 줄이는 것으로 오차는 다음과 같이 표현할 수 있다.

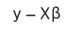
오차 L2노름을 선형회귀 목적식으로 하면 다음과 같은 그레디언트 벡터를 구할 수 있다.

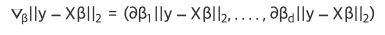
풀어보면, Xβ를 계수 β에 대해 미분하면 X^T가 나온다는 것을 알수도 있다.

그래서, 목적식을 최소화 하는 과정은 다음과 같다.

제곱을 넣어 루트를 벗겨내면 더 간단한 식을 얻을 수 있게된다.

코드로 다음과 같이 나타낼 수 있다.

for t in range(T):
    err = y - X @ beta
    grad = - X.T @ err
    beta = beta - lr * grad

 

 

선형회귀는 역행렬을 구하지 않고도 해를 찾을 수 있게 도와준다.

하지만, 미분 가능하고 볼록한 함수에 대해서만 답을 찾을 수 있다는 한계가 있다.

 

확률적 경사 하강법 (Stochastic Gradient Descent)

데이터의 일부만 가지고 변수를 업데이트하는 기법이다.

볼록이 아닌 목적식에 적합할 수 있다.

출처 : https://www.researchgate.net/figure/Stochastic-gradient-descent-compared-with-gradient-descent_fig3_328106221

전체 데이터에서 미니배치(X(b), y(b))를 뽑아 학습한다.

데이터의 개수가 줄어서 연산량도 줄어든다.

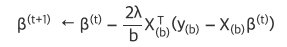
신경망

신경망도 행렬의 연산으로 표현할 수 있다.

아래와 같다.

 

시그마(σ)는 활성함수를 의미하며 활성함수에는 sigmoid, tanh, ReLU가 있다.

 

소프트맥스

소프트맥스 연산은 벡터의 값을 확률로 변환해준다.

예컨데 아래와 같은 식이다.

V = [1,2,1]
softmax(V) = [0.25, 0.5, 0.25]

이 값으로 신경망 모델의 출력을 확률로 표현할 수 있게 된다.

또, 분류문제 같은 경우는 one hot 연산을 이용해 가장 큰 값만 구할 수 있다.

V = [1,2,1]
one_hot(V) = [0, 1, 0]

 

소감

오늘은 멘토님을 만나뵙게 되어 좋았다.
다음주에 멘토님의 인생에 대해 말씀해주신다고 해서 기대하고 있다.

그리고 단톡방을 만들었는데, 팀원들과 좀 더 친해질 수 있을 것 같다.

 

AI Math를 수강하며 원래 알고있던 내용도 보충할 수 있었고,

내가 놓친 부분을 다른 캠퍼 분들이 집어주셔서 좋았다.