[컨볼루션] ShuffleNet

*본 내용은 공부 정리용으로 작성되었으며, 내용에 오류가 있을 수도 있습니다.

ShuffleNet

ShuffleNet은 기존 MobileNet과 같은 이유로 만들어졌다. 주요 목적은 변수와 연산량을 줄이는 것으로, MobileNet에선 Depth-wise separable convolution을 썼지만 이번엔 Group convolution과 Channel Shuffle을 사용한다.

 

MobileNet과 Depth-wise separable convolution, Group convolution에 대해선 이전에 포스팅 한 것이 있다.

 

Group convolution

 

Group Convolution은 전에 AlexNet에서 사용되었는데, 그 때에는 GPU의 성능 한계 때문에 병렬처리를 위해 channel을 나누었던 것이다. 그런데 성능이 좋아서 Group Convolution이 이후에 사용이 되었던 것이다.

 

사실 ShuffleNet은 MobileNet를 더 강화하고자 만들어 졌다.

MobileNet은 Depthwise separable Convolution에서 Pointwise Convolution을 할 떄(1x1 필터를 적용할때) 채널 수에 따른 연산 부담이 크다.

 

일단, Depthwise separable Convolution을 할 때의 연산량은 다음과 같다. (K = 필터크기, N = 출력채널크기, Iw, Ih = 입력크기, M = 입력채널크기)

 

$$ K^{2}MI_{w}I_{h} + NMI_{w}I_{h} $$

 

여기서 덧셈을 기점으로 뒷 부분이 Poinwise Convolution에 대한 연산량인데, K, 필터크기가 아무리 커봤자 5x5 정도 밖에 안되기 때문에 N, 출력채널크기에 따라 연산량이 좌우된다.

 

그 말은, 특성맵을 많이 늘릴 수 없다는 것이다.

 

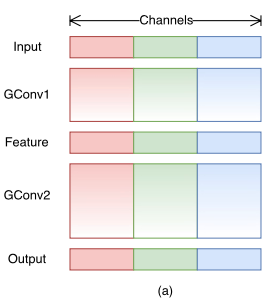
따라서 이점을 해결하기 위해, Group Convolution을 사용했다.연산량을 줄이려면, 출력채널크기를 줄이지 않고 더 많은 그룹으로 나누면 되니, 특성맵 크기를 많이 늘릴 수 있다.

 

연산량은 다음과 같다. (K = 필터크기, N = 출력채널크기, M = 입력채널크기, g = 그룹 개수)

 

$$g*K^2 \frac{N}{g} * \frac{M}{g} = \frac{K^2NM}{g}$$

 

하지만. 채널별로 그룹 나누기를 하면, 각각 별개의 망으로 학습을 하니, 여러 특성에 얽힌 복합적인 정보를 고려할 수 없게 된다.

 

이 문제를 해결하는 방법이 아래 나와있다.

channel shuffle

channel shuffle은 채널들을 골고루 섞어서 다시 재조합 한다면, 서로 영향을 끼치게 된다는 것이다.이렇게 섞는 연산과정은 다음과 같다.

 

$g=3$개의 그룹으로 나눠진 $N/g=3$크기의 채널들이 아래와 같다고 해보자. (A,B,C가 그룹 1,2,3이 채널 크기)

$$\begin{bmatrix} A_1 & A_2 & A_3 & B_1 & B_2 & B_3 & C_1 & C_2 & C_3 \end{bmatrix}$$

여기서 $(g, N/g)$으로 reshape를 한다.

$$\begin{bmatrix} A_1 & A_2 & A_3 \\ B_1 & B_2 & B_3 \\ C_1 & C_2 & C_3 \end{bmatrix}$$

그 후, transpose 연산을 취해준다.

$$\begin{bmatrix} A_1 & B_1 & C_1 \\ A_2 & B_2 & C_2 \\ A_3 & B_3 & C_3 \end{bmatrix}$$

다시 flatten 연산을 하면,

$$\begin{bmatrix} A_1 & B_1 & C_1 & A_2 & B_2 & C_2 & A_3 & B_3 & C_3 \end{bmatrix}$$

 

채널들이 골고루 섞이게 된다. (위에선 채널당 맵의 크기가 1x1라고 했지만, 그룹까지 고려해 4차원으로 생각해보자)

 

ShuffleNet Unit

ShuffleNet은 위의 과정을 하나의 Unit으로 구성했다.

a는 depthwise conv를 이용한 bottleneck 구조, b는 Channel Shuffle을 추가한 구조이고, c는 stride=2로 해서 출력을 1/2으로 줄이는 구조이다.

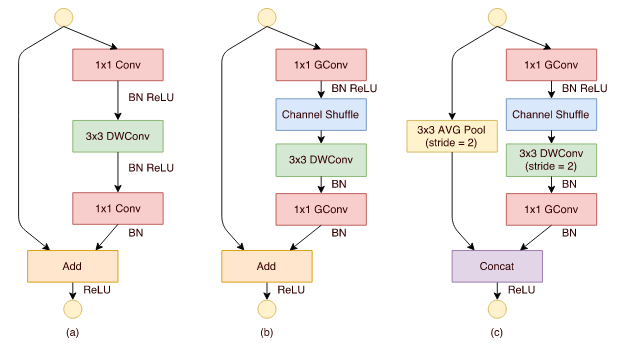
연산량의 차이는 어떨까?

 

a는 다음과 같다. (N = hidden채널크기, M = 입력&출력채널크기, Iw, Ih = 입력크기)

$$NMI_{w}I_{h} + 3^{2}NI_{w}I_{h} + MNI_{w}I_{h} = 2NMI_{w}I_{h} + 9NI_{w}I_{h}$$

 

b는 다음과 같다. (g = 그룹개수)

$$\frac{NMI_{w}I_{h}}{g} + 3^{2}NI_{w}I_{h} + \frac{MNI_{w}I_{h}}{g} = \frac{2NMI_{w}I_{h}}{g} + 9NI_{w}I_{h}$$

 

c는 다음과 같다.

$$\frac{NMI_{w}I_{h}}{g} + \frac{3^{2}NI_{w}I_{h}}{2^2} + \frac{MNI_{w}I_{h}}{2^{2}g} = \frac{5NMI_{w}I_{h}}{4g} + \frac{9NI_{w}I_{h}}{4}$$

 

Experiments

결과는 어떠할까? 아래의 Net 1x, 0.5x, 0.25x는 채널의 수를 의미한다.

g, 그룹수가 증가할 수록 에러가 줄어드는 효과를 보인다.

 

 

셔플을 적용한 경우와 적용하지 않은 경우도 차이를 보인다. (적용한 경우가 더 나은 성능을 보인다)

 

 

비슷한 크기의 MobileNet과 비교했을 때도 좋은 성능을 보인다고 하고 있다.

 

 

같은 오류율 대비 복잡도를 비교해봐도 경량화가 잘 된것을 보여주고 있다.

 

 

-참고-

rxiv.org/pdf/1707.01083.pdf

hichoe95.tistory.com/54

openresearch.ai/t/shufflenet-an-extremely-efficient-convolutional-neural-network-for-mobile-devices/59