[컨볼루션] Depthwise separable convolution

* 본 내용은 공부 정리용으로 작성된 것이며 오류가 있을 수 있습니다.

 

Nomal Convolution

기존 convolution

 

기존 convolution에서 연산량은 아래와 같다. (K = 필터크기, N = 출력채널크기, Iw, Ih = 입력크기, M = 입력채널크기)

 

$$ K^{2}MNI_{w}I_{h} $$

 

따라서 위의 예제의 연산량은 $ 3^2*N*3*8*8 = 1,728N $ (N=1)이다.

 

이렇게 출력 채널이 작아지는 경우도 있지만, 특성지도를 더 늘리기 위해 채널의 수를 늘리는 경우도 있다. (N>1인 경우)

 

N을 다른 방식으로 처리해서 기존 방식보다 곱셈연산을 줄인 방식이 아래에 나와있다.

Dept-wise convolution

Depth-wise convolution은 채널을 분리해서 컨볼루션 연산을 적용한 뒤, 다시 합치는 방식이다.

이렇게 하면, 곱셈의 양이 줄어든다.

 

기존 convolution에서 연산량은 아래와 같다. (K = 필터크기, Iw, Ih = 입력크기, M = 입력채널크기)

 

$$ K^{2}MI_{w}I_{h} $$

 

따라서 위의 예제의 연산량은 $ 3^{2}*3*8*8 = 1,728$이다.

 

Depth-wise convolution을 수행 한 후, N을 그 다음에 처리한다.

Point-wise convolution

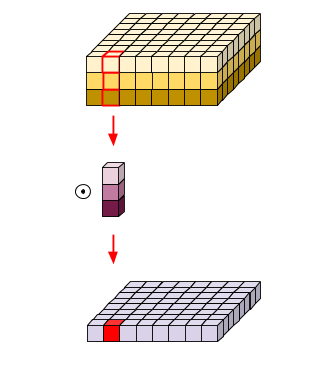
각각 따로 convolution을 수행한 결과들을 채널이 N인 결과로 바꿔야 한다.

여기서는 공간은 처리하지 않고 채널만 처리한다.

 

Point-wise convolution의 연산량은 다음과 같다. (Iw, Ih = 입력크기, N = 출력 채널의 크기, M = 입력채널크기)

 

$$ NMI_{w}I_{h} $$

 

위의 예제의 연산량은 $ N*3*8*8 = 192N$(N=1) 이다.

Depth-wise separable convolution

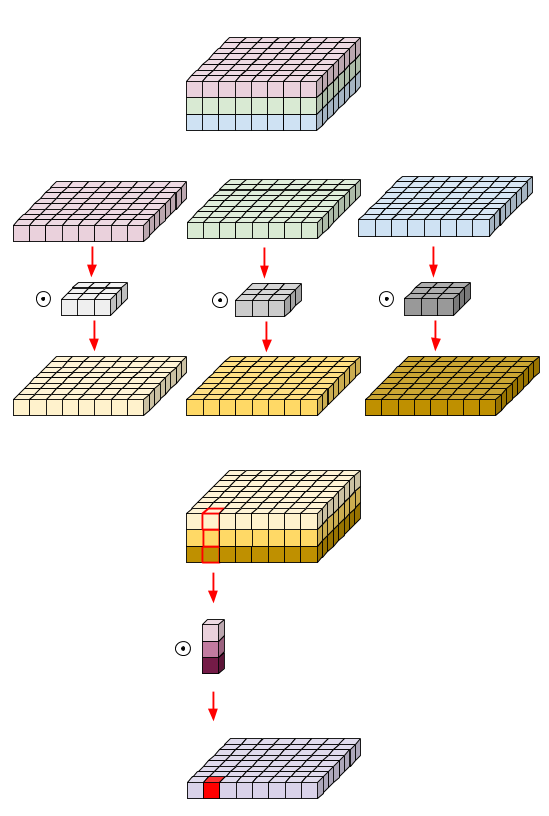
이러한 일련의 과정을 거친 것이 Depth-wise separable convolution 이다.

공간영역에 conv를 적용한 뒤, 채널영역에 conv를 적용한다는 것이 이 방식의 핵심이다.

 

총 연산량은 아래와 같다. (K = 필터크기, N = 출력채널크기, Iw, Ih = 입력크기, M = 입력채널크기)

 

$$ K^{2}MI_{w}I_{h} + NMI_{w}I_{h} $$

 

위의 예제에서는 $ 3^{2}*3*8*8 + N*3*8*8 = 1,728 + 192N$(N=1) 이다.

 

기존의 Convolution과 비교하면 얼마나 연산량이 줄었을까?

 

$1,728N$ vs $1,728 + 192N$

 

N 즉, 출력채널이 커질 수록 Depth-wise separable convolution이 훨씬 빠르다.

 

하지만 이 방법도 만능은 아니다. 이렇게 하면 각 특성간의 컨볼루션 연산이 잘 이루어지지 않기 때문이다.

 

또한, K, 필터크기가 아무리 커봤자 5x5 정도 밖에 안되기 때문에 N, 출력채널크기에 따라 연산량이 좌우된다.

따라서, 경량화를 했다고 하지만, 출력 채널크기를 많이 늘릴 수는 없을 것이다.

 

 

 

 

 

사진 출처 : https://medium.com/@zurister/depth-wise-convolution-and-depth-wise-separable-convolution-37346565d4ec